Question

2. Suppose that a parallel-plate capacitor has circular plates with radius R = 30 mm and a plate separation of d = 5.0 mm. Suppose also that a sinusoidal potential difference with a maximum value and a frequency of =60 Hz is applied across the plates. Find , the maximum value of the induced magnetic field that occurs at r = R. Express your answers in terms of variables first and then plug in numbers afterword.

Answer 1

The maximum value of the induced magnetic field is
`2.901*10^(-13)\ T`.

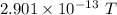Step-by-step explanation:

Given that,

Radius of plate = 30 mm

Separation = 5.0 mm

Frequency = 60 Hz

Suppose the maximum potential difference is 100 V and r= 130 mm.

We need to calculate the angular frequency

Using formula of angular frequency

`\omega=2\pi f`

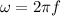
Put the value into the formula

`\omega=2*\pi*60`

`\omega=376.9\ rad/s`

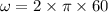
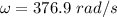
When r>R, the magnetic field is inversely proportional to the r.

We need to calculate the maximum value of the induced magnetic field that occurs at r = R

Using formula of magnetic filed

`B_(max)=(\mu_(0)\epsilon_(0)R^2*V_(max)*\omega)/(2rd)`

Where, R = radius of plate

d = plate separation

V = voltage

Put the value into the formula

`B_(max)=(4\pi*10^(-7)*8.85*10^(-12)*(30*10^(-3))^2*100*376.9)/(2*130*10^(-3)*5.0*10^(-3))`

`B_(max)=2.901*10^(-13)\ T`

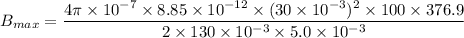
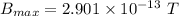
Hence, The maximum value of the induced magnetic field is
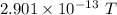`2.901*10^(-13)\ T`.