Question

Write the equation of a line that is perpendicular to y = 7/5 x + 6 y= 5/7and that passes through the point ( 2 , − 6 )

Answer 1

Equation of a line perpendicular to
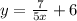`y = (7)/(5x) + 6` and passes through the point ( 2 , − 6 ) is 5x – 7y = 4.

Step-by-step explanation:

Need to write equation of line perpendicular to y = 7/5x + 6 and passes through the point ( 2 , − 6 )

Generic slope intercept form of a line is given by y = mx + c , where m = slope of the line.

On comparing the given slope intercept form of given equation with generic slope intercept form y = mx + c , we can say that for line
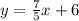`y = (7)/(5)x + 6`, slope m = 7/5

Product of slope of perpendicular line is -1 .

Let say slope of required line perpendicular to y = 7/5x + 6 is represented by m1

And as Product of slope of perpendicular line is -1 .

=>
`m * m1 = -1`

=>
`(7)/(5)* m1 = -1`

=>
`m1 = (-5)/(7)`

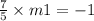
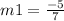
so now we need to find the equation of a line whose slope is
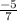`(-5)/(7)` and passing through (2 , -6).

Equation of line passing through (x1 , y1) and having slope of m is given by

(y – y1) = m (x – x1)

In our case x1 = 2 and y1 = -6 and m = -5/7

Substituting the values in equation of line we get

=>
`(y-(-6)) = (-5)/(7) (x-2)`

=>
`y +6= (-5)/(7) x + (10)/(7)`

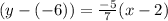
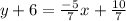
=> 7(y +6) = -5x +10

=> 5x – 7y = 10 – 6

=> 5x – 7y = 4

Hence equation of a line perpendicular to
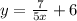`y = (7)/(5x) + 6` and passes through the point ( 2 , − 6 ) is

5x – 7y = 4.