Question

A random sample of 150 towns in a western state had a mean annual precipitation of 2.86 inches. Assume that the population standard deviation is known to be 0.78 inches. Compute the 95% confidence interval for μ Select one: a. 2.51 to 3.53 inches b. 2.74 to 2.98 inches c. 2.43 to 3.79 inches d. 2.31 to 3.88 inches

Answer 1

b. 2.74 to 2.98 inches

Explanation:

Confidence Interval can be calculated using M±ME where

• M is the mean annual precipitation (2.86 inches)
• ME is the margin of error from the mean

And margin of error (ME) can be calculated as

ME=
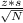`(z*s)/(√(N) )` where

• z is the corresponding statistic in 95% confidence level (1.96)

• s is the standard deviation of the population (0.78)

• N is the number of towns sampled (150)

Putting the numbers, we get:

ME=
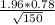`(1.96*0.78)/(√(150) )` ≈ 0.1248

95% Confidence Interval would be 2.86±0.12 or 2.74 to 2.98 inches