Question

In a particular illness , a false-positive result is obtained about 1 in 125 times the test is administered. If the test is administered to 15,000 people, estimate the probabilty of there being more than 135 false-positive results.

(HINT: use the normal approximation to the binomial distribution)

Answer 1

0.0778

Explanation:

Probability of false positive result, p =
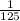`(1)/(125)` = 0.008

Sample size, n = 15,000

mean, μ = np = 15000 × 0.008 = 120

Now,

Standard deviation, σ =
`√(np(1-p))`

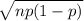
or

=
`√(15,000*0.008(1-0.008))`

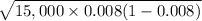
= 10.91

Now,

Probability of there being more than 135 false-positive results

= P(X > 135) ≈
`P((X-\mu)/(\sigma)>(135-120)/(10.91))`

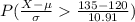
or

= P(z > 1.42)

or

= 1 - P(z ≤ 1.42)

= 1 - 0.9222 [P(z ≤ 1.42) = 0.9222 from standard z table]

= 0.0778

Hence,

P(X > 135) = 0.0778