Question

For males the expected pulse rate is 70 per second and the standard deviation is 10 per second. For women the expected pulse rate is 77 per second and the standard deviation is 12 per second. Let !X ¼ the sample average pulse rate for a random sample of 40 men and let !Y ¼ the sample average pulse rate for a random sample of 36 women.What is the approximate distribution of \overline{X}-\overline{Y} ? Justify your answer.

Answer 1

Normal

Explanation:

Given are the pulse rates average and std deviation for men and women.

Men Women Difference

Pulse rate per second 70 77 -7

Std dev per second 10 12

Variance 100 144 244

n 40 36

Variance/n 2.5 4 6.5

Std error 2.549509757

The first one represents X that of men and ii one that of women Y.

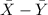`\bar X -\bar Y` is Normal

Mean = difference in means

and Std dev of difference =
`\sqrt{(\sigma_1^2 )/(n_1) +(\sigma_2^2 )/(n_2)}`

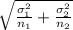
Thus using the above we calculate the distribution of difference of means is Normal with mean = -7 and std error = 2.5495