Answer:
Rise in level of fluid is 0.11 m
Rise in level of fluid in case of mercury is 0.728 cm or 7.28 mm
Solution:
As per the question:
Density of oil,
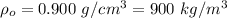
Change in Pressure in the tank,
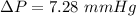
Density of the mercury,

Now,
To calculate the rise in the level of fluid inside the manometer:
We know that:
1 mmHg = 133.332 Pa
Thus
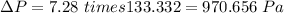
Also,
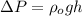
where
g = acceleration due to gravity
h = height of the fluid level
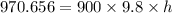
h = 0.11 m
Now, if mercury is used:
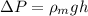
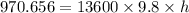
h = 0.00728 m = 7.28 mm