Answer:
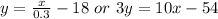
is the equation of perpendicular line.
Explanation:
We are given , the equation of a line is
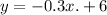
We can deduce that the slope of the given line is
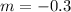
The slope of its perpendicular line would be ,
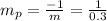
Now using the point slope form,
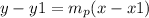
Use the given point
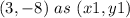 substituing these.
substituing these.
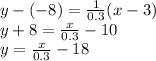
Therefore the required equation of a line that is perpendicular to y=-0.3x. +6 and that passes through the point (3,-8) is y=\frac{x}{0.3} -18[/tex]