Question

The completion time for an exam is normally distributed with expected value 75 minutes and variance 12 minutes. What is the probability that a student will finish this exam in less than 70 minutes or more than 80 minutes?

Answer 1

14.89% or 0.1489

Explanation:

First, find the z-score for both 70 and 80 minutes and their corresponding percentile.

`z= (X - \mu )/(SD) \\SD=√(V) =√(12)\\\mu =75\\z= (X - 75)/(√(12))\\\\`

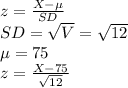
For X = 70 minutes:

`z= (70 - 75)/(√(12))\\z=-1.4434`

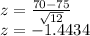
This z-score is equivalent to the 7.445 th percentile, so the probability of a student finishing this exam in less than 70 minutes is 7.445%

or X = 80 minutes:

`z= (80 - 75)/(√(12))\\z=1.4434`

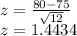
This z-score is equivalent to the 92.555 th percentile, so the probability of a student finishing this exam in more than 80 minutes is 100- 92.555 = 7.445%

Therefore, the probability (P) of a student finishing this exam in less than 70 minutes or more than 80 minutes is:

P = 7.445% + 7.445% = 14.89%