Question

A car leaving a stop sign accelerates constantly from a speed of 0 feet per second to reach a speed of 44 feet per second. The distance of the car from the stop sign, d d , in feet, at time t t , in seconds, can be found using the equation d=1.1 t 2 d=1.1t2 . What is the average speed of the car, in feet per second, between t=2 t=2 and t=5 t=5 ? 5.5 6.6 7.7 8.5

Answer 1

Option C.

Explanation:

The distance of the car from the stop sign, d , in feet, at time t , in seconds, can be found using the equation

`d=1.1t^2`

The average rate of change of a function f(x) on [a,b] is

`m=(f(b)-f(a))/(b-a)`

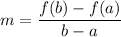
We need to find the average speed of the car, in feet per second, between t=2 and t=5.

At t=2,

`d=1.1(2)^2=4.4`

At t=5,

`d=1.1(5)^2=27.5`

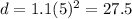
The average speed of the car, in feet per second, between t=2 and t=5 is

`\text{Average speed}=(d(5)-d(2))/(5-2)`

`\text{Average speed}=(27.5-4.4)/(3)`

`\text{Average speed}=(23.1)/(3)`

`\text{Average speed}=7.7`

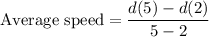
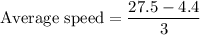
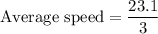
The average speed of the car, in feet per second, between t=2 and t=5 is 7.7 feet per second.

Therefore, the correct option is C.