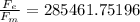Question

Compare the gravitational force on a 1.0-kg apple that is on the surface of Earth versus the gravitational force due to the Moon on the same apple in the same location on the surface of Earth.

Assume that Earth and the Moon are spherical and that both have their masses concentrated at their respective centers.
Mass of the Moon is 7.35 ×× 1022 kg. Orbit radius of the Moon is 3.84 ×× 108 m.

What is the ratio of the force between Earth and the apple to the force between Moon and the apple?

Answer 1

`(F_e)/(F_m)=285461.75196`

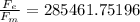
Step-by-step explanation:

r = Radius of Earth =
`6.371* 10^6\ m`

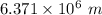
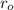`r_o` = Radius of Moon =
`3.84* 10^(8)\ m`

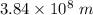
G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

Gravitational force on the apple on Earth

`F_e=(GM_em)/(r^2)`

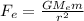
Gravitational force of Moon on the apple

`F_m=(GM_mm)/(r_m^2)\\\Rightarrow F=(GM_mm)/((r_o-r)^2)`

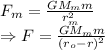
Dividing the two equations

`(F_e)/(F_m)=((GM_em)/(r^2))/((GM_mm)/((r_o-r)^2))\\\Rightarrow (F_e)/(F_m)=(M_e* (r_0-r^2))/(r^2M_m)\\\Rightarrow (F_e)/(F_m)=(5.972* 10^(24)* (3.84* 10^(8)-6.371* 10^6)^2)/((6.371* 10^6)^2* 7.35* 10^(22))\\\Rightarrow (F_e)/(F_m)=285461.75196`

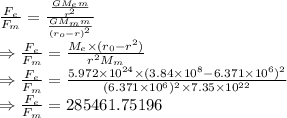
The ratio of the force between Earth and the apple to the force between Moon and the apple is
`(F_e)/(F_m)=285461.75196`