Question

In a certain experiment, the error made in determining the density of a substance is a random variable having a uniform density with a=-0.015 and b=0.015. Find the probability that such errors will be between –0.002 and 0.003

Answer 1

The required probability is 0.1667

Explanation:

Consider the provided information.

According to Probability Density Function:
`f(x)\left\{\begin{matrix} (1)/(b-a)& a<x<b\\ 0 & elsewhere\end{matrix}\right.`

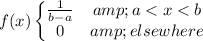
Therefore,

`f(x)\left\{\begin{matrix} (1)/(0.030)& -0.015<x<0.015\\ 0 & elsewhere\end{matrix}\right.`

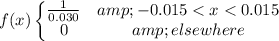
The probability that such errors will be between –0.002 and 0.003 is:

`P(-0.002\leq x\leq 0.003)=\int\limits^(0.003)_(-0.002) {(1)/(0.030)} \, dx`

`P(-0.002\leq x\leq 0.003)=(1)/(0.030)[x]^(0.003)_(-0.002)`

`P(-0.002\leq x\leq 0.003)=(0.003+0.002)/(0.030)=0.1667`

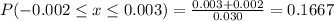
Hence, the required probability is 0.1667