Answer:
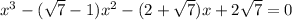
Explanation:
We have to find the equation of a polynomial whose roots are - 2, 1 and √7.
It will be a single variable three-degree equation.
Let the variable is x.
So, (x + 2), (x - 1) and (x - √7) will be the factors of the equation.
Therefore, the equation can be written as
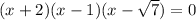
⇒
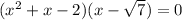
⇒
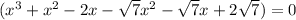
⇒
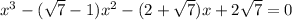
So, this is the required equation. (Answer)