Question

Find the maximum profit and the number of units that must be produced and sold in order to yield the maximum profit. Assume that​ revenue, Upper R left parenthesis x right parenthesisR(x)​, and​ cost, Upper C left parenthesis x right parenthesisC(x)​, of producing x units are in dollars. Upper R left parenthesis x right parenthesisR(x)equals=4 x4x​, Upper C left parenthesis x right parenthesisC(x)equals=0.01 x squared plus 0.3 x plus 40.01x2+0.3x+4

Answer 1

185 units

Explanation:

Given,

The revenue function is,

`R(x) = 4x`

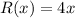
Cost function,

`C(x) = 0.01x^2 + 0.3x + 4`,

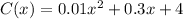Where,

x = number of units produced.

Thus, profit = revenue - cost

`P(x) = 4x - ( 0.01x^2 + 0.3x + 4) = -0.01x^2 + 3.7x - 4`

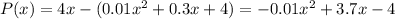
Differentiating with respect to x,

`P'(x) = -0.02x + 3.7`

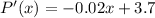
Again differentiating with respect to x,

`P''(x) = -0.02`

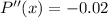
For maxima or minima,

P'(x) = 0,

`-0.02x + 3.7x =0`

`-0.02x = -3.7`

`\implies x = (3.7)/(0.02)=185`

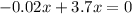
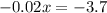
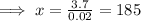
For x = 185,

P''(x) = negative,

Hence, for maximising the profit 185 units must be produced.