Answer: d. 0.0019
Explanation:
Given : The weight of potato chips in a medium-size bag is stated to be 10 ounces.
The amount that the packaging machine puts in these bags is believed to have a Normal model with mean 10.2 ounces and standard deviation 0.12 ounces.
i.e.
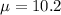 and
and

Let x represents the weight of potato chips in a medium-size bag.
The probability that the mean weight of the 3 bags (i.e. sample size = 3) is below the stated amount will be :-
![P(x<10)=P((x-\mu)/((\sigma)/(√(n)))<(10-10.2)/((0.12)/(√(3))))\\\\=P(z<-2.89)=1-P(z<2.89)\ \ [\because P(Z<-z)=1-P(Z<z)]\\\\=1-0.9981=0.0019 \ \ \text{[By using z-value table]}](https://img.qammunity.org/2020/formulas/mathematics/college/uvyjs9cjlk9h2714x7a3217ku5u33818o0.png)
Hence, the required probability =0.0019