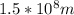To solve the exercise it is necessary to take into account the concepts of wavelength as a function of speed.
From the definition we know that the wavelength is described under the equation,
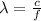
Where,
c = Speed of light (vacuum)
f = frequency
Our values are,
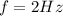
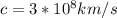
Replacing we have,
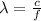
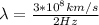
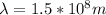
Therefore the wavelength of this wave is