Question

An airplane pilot is fertilizing a field. The height y in feet of the fertilizer t seconds after it is dropped is modeled by y(t) = −16t2 − 3t + 300. The horizontal distance x in feet between the fertilizer and its dropping point is modeled by x(t) = 85t. At approximately what horizontal distance from the field should the pilot start dropping the fertilizer?

Answer 1

About 360.178 feet

Explanation:

So we want the vertical distance between the fertilizer and the ground to be 0.

This going to be about the time the pilot has dropped it

So we first need to find when y is 0.

`0=-16t^2-3t+300`

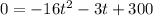
We are going to use the quadratic formula to solve for t:

`a=-16`

`b=-3`

`c=300`

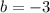
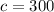
The quadratic formula is:

`t=(-b \pm √(b^2-4ac))/(2a)`

`t=(3 \pm √((-3)^2-4(-16)(300)))/(2(-16))`

`t=(3 \pm √(9+19200))/(-32)`

`t=(3 \pm √(19209))/(-32)`

`t=(3+√(19209))/(-32) \text{ or } (3-√(19209))/(-32)`

`t \approx -4.424891774 \text{ or } 4.237391774`

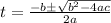
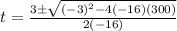
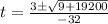
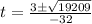
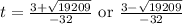
So the pilot has released it at about 4.237391774 seconds since the fertilizer has actually hit the ground at roughly this time.

So we want to know the horizontal distance at t=4.237391774:

`85t`

`85(4.237391774)`

`360.1783008`

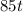
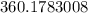
360.178 feet