Question

What are the approximate values of the non-integral roots of the polynomial equation? –5.57 –1.95 0.21 1.27 4.73

Answer 1

D. 1.27

E. 4.73

Answer 2

Option 4 and 5.

Explanation:

Consider the given polynomial equation is

`x^(4)-4x^(3)=6x^(2)-12x`

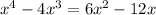
We need to find approximate values of the non-integral roots of the polynomial equation.

`x^(4)-4x^(3)-6x^(2)+12x`

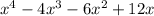
Find factor form.

`x(x^(3)-4x^(2)-6x^(1)+12)`

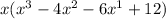
For x=-2 the value of parenthesis is 0. It means (x+2) is a factor of parenthesis.

Divide the parenthesis by (x+2). After division remainder is 0 and quotient is
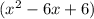`(x^2 - 6 x + 6)`, so the factor form is

`x (x + 2) (x^2 - 6 x + 6)`

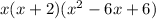
Equate the factor form equal to 0, to find the roots.

`x (x + 2) (x^2 - 6 x + 6)=0`

`x=0`

`x+2=0\Rightarrow x=-2`

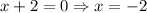
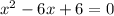`x^2 - 6 x + 6=0` .... (1)

Quadratic formula for
`ax^2+bx+c=0` is

`x=(-b\pm √(b^2-4ac))/(2a)`

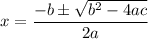
In (1), a=1, b=-6, c=6. Using quadratic formula we get

`x=(-(-6)\pm √((-6)^2-4(1)(6)))/(2(1))`

`x=(6\pm √(12))/(2)`

`x=(6\pm 2√(3))/(2)`

`x=3\pm √(3)`

`x=3+1.73, 3-1.73`

`x=4.73, 1.27`

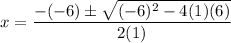
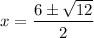
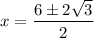
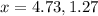
The approximate values of the non-integral roots of the polynomial equation are 4.73 and 1.27.

Therefore, the correct options are 4 and 5.