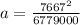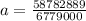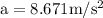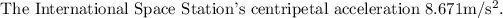Question

Warmup: The International Space Station is orbiting with a velocity of 7,667 m/s at an altitude of 408,000 m. The radius of Earth is 6,371,000 m. What is the ISS's centripetal acceleration?

Answer 1

`8.671 \mathrm{m} / \mathrm{s}^(2)` is the centripetal acceleration.

Step-by-step explanation:

As per given values

Radius of earth (r) = 6371000 m

The "international space station" is orbiting with a velocity (v) = 7667 m/s.

"Centripetal acceleration" is the acceleration is equal to "the square of the velocity" divided by "the radius of the circular path".

`\text { Centripetal acceleration a }=(V^(2))/(R)`

V = velocity of the orbit

R = radius of the earth + height of the space station

R = 6,371,000 + 408,000

R = 6779000 m

The direction of the centripetal acceleration is always inwards along the radius vector of the circular motion.

`a=(7667^(2))/(6779000)`

`a=(58782889)/(6779000)`

`\mathrm{a}=8.671 \mathrm{m} / \mathrm{s}^(2)`

`\text { The International Space Station's centripetal acceleration } 8.671 \mathrm{m} / \mathrm{s}^(2).`