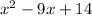I didn't get all the part with the tiles, but here's the general answer:
given a polynomial
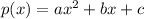
we have that
 is a factor of
is a factor of
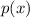 if and only if k is a root of
if and only if k is a root of
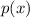 , i.e. if
, i.e. if
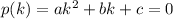
So, given the polynomial
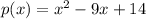
We can check if
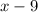 is a factor by evaluating
is a factor by evaluating
 :
:
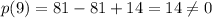
So,
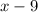 is not a factor.
is not a factor.
Similarly, we can evaluate
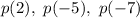 to check if
to check if
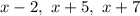 are factors:
are factors:

So, only
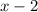 is a factor of
is a factor of