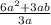Answer:
Part 1 =
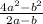
Part 2 =
Explanation:
Let the fraction be denoted by numerator and denominator then given denominator for the first expression contains 2a-b.
let us assume that the numerator contains x
now given that 2a+b is the value of the expression which means
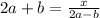
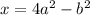
Therefore the fraction for the first option is
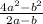
Given the denominator for the second expression is 3a.
Let us assume that the numerator contains x
Now given that 2a+b is the value of the expression which means
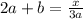
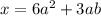
Therefore the fraction for the second option is