Answer:
Part a)
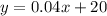
Part b) The total cost is $31
Part c) The total cost is $48
Explanation:
Part a) Write an algebraic expression to represent the total cost
Let
x -----> the number of minutes for all calls in a month
y ----> the total cost in dollars per month
we know that
The linear equation in slope intercept form is equal to

where
m is the slope or unit rate of the linear equation
b is the y-intercept or initial value of the linear equation
In this problem we have
The unit rate or slope is equal to
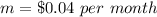
The initial value or y-intercept (value of y when the value of x is equal to zero) is
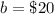
substitute
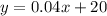
Part b) How much will it cost to use 275 minutes in one month?
For x=275 minutes
substitute the value of x in the linear equation and solve for y

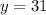
therefore
The total cost is $31
Part c) How much will it cost to use 700 minutes in one month?
For x=700 minutes
substitute the value of x in the linear equation and solve for y
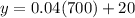
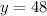
therefore
The total cost is $48