Question

Given the acceleration, initial velocity, and initial position of a ball thrown vertically upward, how long does it take for it to reach its maximum height? What is the maximum height?

Answer 1

`t = (v_(o) )/(g)`

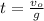
ymax= y₀ + v₀²/2g

Step-by-step explanation:

The equations of uniformly accelerated rectilinear motion of upward (vertical) for the y axis are :

vfy = v₀y-gt Formula (1)

vfy² = v₀y²-2gΔy Formula (2)

Where:

t: time in any position (s)

Δy= y-y₀

y = vertical position in any time (m)

y₀ : initial vertical position in meters (m)

v₀y: initial vertical velocity in m/s

vfy: final vertical velocity in m/s

g: acceleration due to gravity in m/s²

Data

v₀y = v₀ : total initial speed of the ball

y₀ : initial vertical position of the ball

g :acceleration due to gravity

Time (t) calculation for the ball to reach maximum height

We apply the formula (1)

vfy = v₀y-gt

When the ball reaches its maximum height (h), vy = 0:

0= v₀-gt

v₀ = gt

`t = (v_(o) )/(g)`

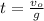
Calculation of the maximum hight that reaches the ball

When the ball reaches its maximum height (ymax), vy = 0:

We apply the formula (2)

vfy²= v₀y²-2gΔy

0= v₀²-2gΔy

2gΔy = v₀²

Δy= v₀²/2g ,Δy= ymax-y₀

ymax-y₀ = v₀²/2g

ymax= y₀ + v₀²/2g