Final answer:
The number of possible 4-digit codes with repetition allowed using the digits 0-9 is
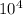 , which equals 10,000 since each position can be filled by any of the ten digits independently.
, which equals 10,000 since each position can be filled by any of the ten digits independently.
Step-by-step explanation:
To determine the number of possible 4-digit codes with repetition allowed using the digits 0-9, one needs to consider that each digit in the code can be any of the ten digits. For each position in the 4-digit code, there are 10 options. Since there are 4 positions, and the choices are independent of each other, the number of different combinations can be found by multiplying the number of options for each position.
The calculation would be: 10 × 10 × 10 × 10 because there are 10 choices for the first digit, 10 choices for the second digit, 10 choices for the third digit, and 10 choices for the fourth digit.
Step-by-Step Calculation
First digit: 10 possibilities
Second digit: 10 possibilities
Third digit: 10 possibilities
Fourth digit: 10 possibilities
Therefore, the total number of possible 4-digit codes is
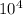 , which is 10,000.1
, which is 10,000.1