Answer:
k=2
Explanation:
Clearly both the functions are straight lines
the equation of straight line passing through the two points (a , b) and (c , d) is
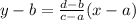
Now f(x) passes through (-4 , 0) and (0 , 4)
the equation is
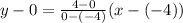
y=x+4
Now g(x) passes through (-2 , 0) and (0 , 4)
the equation is
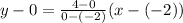
y=2x+4
here f(x)=x+4 and g(x)=2x+4
clearly g(x)=f(2x)
therefore k=2