Answer:
The equation of line with given points is y - 4 = 3 ( x + 2 ) .
Explanation:
Given as :
The points of line are ( 1 , 13 ) and ( - 2 , 4 )
The point slope intercept equation of line is
y -
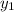 = m ( x -
= m ( x -
 )
)
Where m is the slope of line
So , Slope , m =

Or, m =
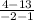
Or, m =

∴ m = 3
Now The equation of line is
y -
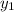 = m ( x -
= m ( x -
 )
)
Or. y - 13 = 3 ( x - 1 )
Or, y - 13 = 3 x - 3
Or, y = 3 x - 3 + 13
∴ y = 3 x + 10
I.e y - 4 = 3 x + 6
Or, y - 4 = 3 ( x + 2 )
Hence The equation of line with given points is y - 4 = 3 ( x + 2 ) . Answer