Question

Slanted sides of a tent are 11 feet long each and the bottom of the tent is 12 feet across. What is the tallest point of the tent?

Answer 1

The tallest point of the tent is 9.22 ft.

Explanation:

The slant sides of the tent are: 11 ft

The base of the tent is 12 ft apart.

Let the height of the tent = h ft

Now, if we assume the tent to be of conical shape, the half of the tent forms a right angles triangle.

In this right angled triangle:

Slant Height of tent = Hypotenuse of the triangle = 11 ft

Height of tent = Perpendicular of the triangle = h

(Base /2) of tent = Base of the triangle = 6 ft

Now, USING PYTHAGORAS THEOREM in a right triangle:

`(Base)^2  + (Perpendicular)^2  = (Hypotenuse)^2`

⇒
`(6)^2  + h^2  = (11)^2\\\implies h^2  = 121 - 36  = 85\\or, h = √(85)  = 9.22`

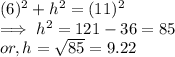
⇒ h = 9.22 ft

Hence the tallest point of the tent is 9.22 ft.