1210 cubic feet
Explanation:
Initial dimensions of the storeroom were
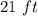 length,
length,
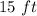 width and
width and
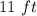 height.
height.
The room is in the shape of a cuboid. Volume of a cuboid =
 , where
, where
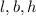 are the length, width and height of the cuboid.
are the length, width and height of the cuboid.
So, Volume of storeroom initially =
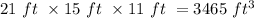
Finally, the length was increased to
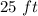 and width to
and width to
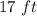 .
.
Final volume of storeroom =
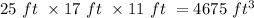
Increase in volume =
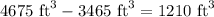
∴ 1210 cubic feet of storage was added.