Answer:
6 cm
Step-by-step explanation:
The lens equation is :
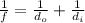
where
 is the focal length,
is the focal length,
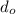 is the distance of the object and
is the distance of the object and
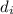 is the distance of the image.
is the distance of the image.
To find the height of the image we first need to find the distance of the image
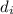 , so we clear for it in the last equation:
, so we clear for it in the last equation:

and since
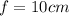 and
and

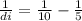
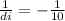
so

Now to find the height of the image we use the magnification:
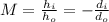
where
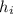 is the image height, and
is the image height, and
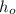 is the object height:
is the object height:
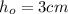
clearing fot
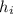 :
:
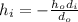
substituting known values:
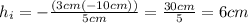
The image height is 6cm.