Question

determine the equation of a line in slope-intercept parallel to 6x+2y=19 and passing through (-6,-13).

Answer 1

`y = - 3x - 31`

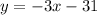
Explanation:

By definition, the slopes of parallel lines are equal. Thus, we need to first five the slope of 6x+2y=19. Recall that slope intercept form is

`y = mx + b`

where m is the slope and b is the y-intercept. So, to find the slope of 6x+2y=19, put it on slope intercept form like so:

6x+2y=19

6x-19=-2y

-3x+19/2=y

So the slope of the line is -3. Then, we will use point slope form to find the equation of the parallel line that passes through (-6, -13). Recall that point slope form is

y-y1=m(x-x1). Using this we find the equation of the parallel line to be:

y+13=-3(x+6)

y+13=-3x-18

y=-3x-31

Thus, the slope of the parallel line is y=-3x-31.

I hope this helps! Cheers!

Answer 2

Answer:
`y=-3x-31`

Explanation:

The equation of the line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope and "b" is the y-intercept.

Given the equation:

`6x+2y=19`

You must solve for "y" in order to express it in Slope-Intercept form:

`2y=-6x+19\\\\y=-3x+(19)/(2)`

You can identify that:

`m=-3`

Since the slopes of parallel lines are equal, then the slope of the other line is:

`m=-3`

Then, you can substitute the slope and the coordinates of the given point into
`y=mx+b` and solve for "b":

`-13=-3(-6)+b\\\\-13-18=b\\\\b=-31`

Therefore, the equation of this line in Slope-Intercept form is:

`y=-3x-31`