Answer:
d = 0.44 kg/m³
Step-by-step explanation:
To determine the density of the gas into the balloon we need to consider the forces that are acting on the balloon in the x (Fx) and y (Fy) components:
x:
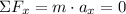
The sum of the forces is zero because there is no force acting on the balloon in this component.
y:
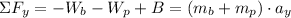 (1)
(1)
where
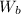 and
and
 : are the weights of the balloon and the package, respectively,
: are the weights of the balloon and the package, respectively,
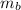 and
and
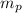 : are the masses of the balloon and the package, respectively, and B: buoyancy force.
: are the masses of the balloon and the package, respectively, and B: buoyancy force.
Knowing that:
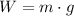 (2)
(2)
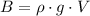 (3)
(3)
where ρ: is the density of the air, g: gravitational acceleration and V: volume of the gas displaced.
And introducing the weights of the balloon and the package from (2), and B from (3) on the equation (1), we can find the mass of the balloon:
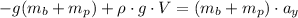
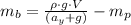
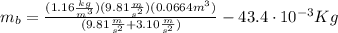
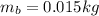
Finally, with the mass of the balloon calculated we can determine the density (d) of the gas inside the balloon:
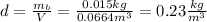
Have a nice day!