Question

A university offers 3 calculus classes: Math 2A, 2B, and 2C. A set of students have each taken at least one of the three classes. 51 have taken Math 2A, 80 have taken Math 2B, and 70 have taken Math 2C. 15 students have taken Math 2A and 2B, 20 have taken Math 2A and 2C, and 13 have taken Math 2B and 2C. Only 4 have taken all three classes. How many students are there in the set?

Answer 1

157 or 156 I don't remember what the number was

Explanation:

Answer 2

157

Explanation:

We are given that

Number of students in maths 2A=n(2A)=51

Number of students in math 2B=n(2B)=80

Number of students in math 2C=n(2C)=70

Number of students in maths 2A and 2B=
`n(A\cap B)=15`

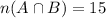
Number of students in maths 2B and 2C=
`n(B\cap C)=13`

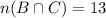
Number of students in maths 2A and 2C=
`n(A\cap C)=20`

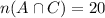
Number of students in maths 2A ,2B and 2C=4

We have to find the number of students in a set.

Formula:
`n(A\cup B\cup C)=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(A\cap C)+n(A\cap B\cap C)`

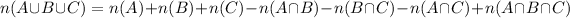
Substitute the values in the given formula

`n(2A\cup 2B\cup 2C)=51+80+70-15-13-20+4=157`

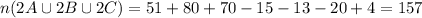
Hence, total number of students in a set=157