Question

A 49.0 kg ice skater is gliding along the ice, heading due north at 4.40 m/s . The ice has a small coefficient of static friction, to prevent the skater from slipping sideways, but μk =0. Suddenly, a wind from the northeast exerts a force of 3.50 N on the skater. Part A Use work and energy to find the skater's speed after gliding 100 m in this wind. Express your answer with the appropriate units.

Answer 1

3.042 m/s

Step-by-step explanation:

To solve this exercise it is necessary to use the Work equation and the conservation of kinetic energy in the Ice skater.

According to the description of the problem, all the work is done from north to south due to the wind direction. In this way, finding the force in this component we have,

`F = 3.50 cos (45) = 2.47 N`

`W = F * d = 2.47 * 100`

`W = 247.48N*m`

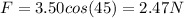
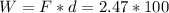
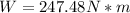
Through the kinetic energy equations we have to

`W = \Delta KE`

`W = KE_i - KE_f`

`KE_f = KE_i - W`

`0.5 m*v_2^2 = 0.5 mv_1^2 - W`

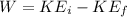
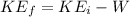
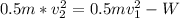
Re-arrange for
`v_2`

`v_2 = \sqrt{v1^2 - 2(W)/(m)}`

`v_2 = \sqrt{(4.4)^2 - 2(247.48)/(49.0)}`

`v_2 = 3.042 m/s`

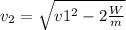
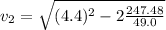
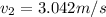
Therefore te speed after gliding 100m in this wind is 3.042m/s