Question

The answer and a short explanation please and quickly​. can anyone help me PLEASE.

Answer 1

The length of AC to the nearest hundredth = 8.06 units.

Explanation:

In the given triangle ABC

CB = 7 units

AB = 4 units

Let AC = h units

Now, using PYTHAGORAS THEOREM in a right angled triangle:

`(BASE)^2  + (PERPENDICULAR)^2  = (HYPOTENUSE)^2`

⇒
`(7)^2 + (4)^4 = h^2\\\implies h^2 = 49 + 16 = 65\\or, h = \sqrt(65) = 8.0622`

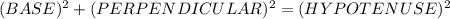
⇒The hypotenuse AC of the given triangle is 8.0622 units.

Rounding off to the nearest hundredth, h = 8.06 units.

Hence, the length of AC = 8.06 units.