Question

The time between calls to a corporate office is exponentially distributed with a mean of 10 minutes.

(a) What is the probability that there are more than three calls in one-half hour?
(b) What is the probability that there are no calls within one half hour?
(c) Determine x such that the probability that there are no calls within x hours is 0.01.

Answer 1

Let X be the time between calls to a corporate office. X has exponential distribution with mean 10 minutes

`\lambda = (1)/(E(X))`

`\lambda = (1)/(10)\ minutes`

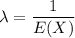
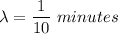
Let Y be the number of calls arrive in one half hour. So Y follows Poisson distribution with parameter

`30 \lambda = 30 (1)/(10)`

`30 \lambda = 3`

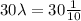
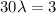
Y follows Poisson distribution with parameter 3. The probability distribution function of Y is ;

P(Y=y) =
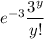`e^(-3) (3^(y))/(y!)` for y=0, 1, 2, 3, ....

a) Probability that there are more than three calls in one-half hour

The number of calls arrive in one hour Y₁ is

`30 \lambda = 30 (1)/(10)`

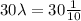
=3

P(Y > 3) = 1 - P(Y ≤ 3)

= 1 - [P(Y = 0) +P(Y = 1) +P( Y = 2) +P( Y = 3)]

=1-[0.0497+ 0.1494+0.2240+0.2240]

= 1- 0.6472

P(Y>3) = 0.3528

b) Probability that there are no calls within one-half hour

P(Y =0) =
`(e^(-3) 3^(0))/(0!)`

P(Y =0) = 0.0498

c) Let x be the number for which probability that there will be no call within x hours is 0.01

`(e^(-6x) 6x^(0))/(0!) =0.01`

`e^(-6x) =0.01`

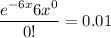
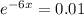
-6 x = ln (0.01)

`x = (-ln(0.01))/(6)`

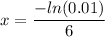
x =0.7675 hrs converting into minutes

X =46.05 minutes