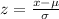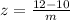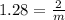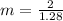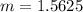Answer:1.5625
Explanation:
Given
mean
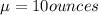
standard deviation
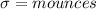
For bottles to be filled over 12 ounces i.e. area right to the bell curve for z score
and area left side of the z score is 1-0.1=0.9
so value close to 0.9 in standard normal curve which is 0.8997
z score corresponding to 0.8997 is 1.28
also z score for 12 ounce