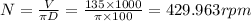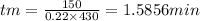Answer:
chip area = 6.908 mm^2
material removal rate 828.96 cm^3/min
power = 40644 kW
MACHINE TIME = 1.585 min
Step-by-step explanation:
GIVEN DATA:
Length 150 mm
diameter vary from 100 to 90 mm
cutting edge angle

speed of cutting is v 135 m/min
feed rate fr = 0.22 min
Ks = 2300 N/mm^2
a) chip area
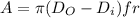
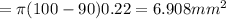
b) material removal rate = chip area * Vc
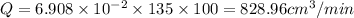
c) power = F* Vc
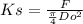

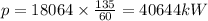
C) Machine time[/tex] tm = \frac{L}{fN}[/tex]