Answer:
16% is the percent of wooden shipping boxes will have breaking strengths greater than 520 pounds per square inch.
Explanation:
We are given the following information:
Mean = 500 pounds
Standard Deviation = 20 pounds
Empirical rule:
- The empirical rule also known as the three-sigma rule or 68-95-99.7 rule
- It is a statistical rule which states that for a normal distribution, almost all data falls within three standard deviations (denoted by σ) of the mean (denoted by µ).
- It shows that 68% falls within the first standard deviation that is
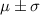
- About 95% of the data lies within the first two standard deviations that is
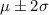
- About 99.7% of the data lies within the first three standard deviations that is
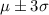
We have to find the percent of its wooden shipping boxes that will have breaking strengths greater than 520 pounds per square inch.
Now,
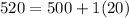
According to empirical rule around 68% of the data will lie between

Thus, 34% of data lies between 500 and 520.
Data lying above 520 = 50% - 34% = 16%
16% is the percent of wooden shipping boxes will have breaking strengths greater than 520 pounds per square inch.