Answer:
(4,-1)
Explanation:
Given
3 Co-ordinates of a parallelogram ABCD
A=(1,-3)
B=(1,0)
C=(4,2)
D=(a,b)
One of the property of a parallelogram is that the diagonals bisect each other
In this case, AC and BD bisect each other, Therefore the middle point of AC and BD coincide
⇒Mid-point of AC= Mid-point of BD
(mid point of 2 points (x,y) and (k,l) is
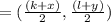 )
)
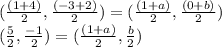
Compare x and y co-ordinates on both sides
⇒
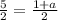
a=4
⇒
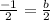
b=-1
Therefore D=(4,-1)