Question

Data from the U.S. Department of Education indicates that 59% of business graduate students from private universities had student loans. Suppose you randomly survey a sample of graduate business students from private universities. Consider the sampling distribution (sample size n = 105) for the proportion of these students who have loans.

What is the mean of this distribution? (Enter your answer accurate to two decimal places.)

What is the standard deviation of this sampling distribution (i.e., the standard error)?

Answer 1

Answer: The mean of this distribution = 61.95

The standard deviation of this sampling distribution (i.e., the standard error= 0.048

Explanation:

Given : Data from the U.S. Department of Education indicates that 59% of business graduate students from private universities had student loans.

i.e. proportion of business graduate students from private universities had student loans : p=0.59

sample size : n=105

Then , the mean of the distribution is given by :-

`\mu= np = (105)(0.59)=61.95`

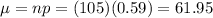
∴The mean of this distribution = 61.95

Then standard deviation of this sampling distribution is given by :-

`\sqrt{(p(1-p))/(n)}\\\\=\sqrt{((0.59)(1-0.59))/(105)}\\\\=√(0.00230381)\\\\=0.047998015832\approx0.048`

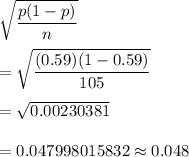
∴The standard deviation of this sampling distribution (i.e., the standard error= 0.048