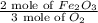Answer : The correct option is (c)
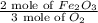
Explanation :
The given balanced chemical reaction is,

From the balanced chemical reaction, we conclude that
As, 3 moles of
 react to give 2 mole of
react to give 2 mole of
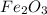
So, 1 mole of
 react to give
react to give
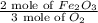 moles of
moles of
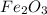
Thus, the conversion factor needed to convert the number of moles of
 to the number of moles of
to the number of moles of
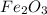 produced is
produced is
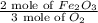
Hence, the correct option is (c)