Unit rates are great for making comparisons between certain things. For example if I was at a grocery store and I wanted to buy steak and I saw 10 ounces for $18 and 12 ounces for $22, I could determine which is a better buy and how much I am saving.
Let me show another example.
70 students in 5 classes = ___ students per class
"Per class" means in one class so we can rewrite the given statement using fractions.
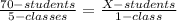
To find out what goes in the blank, notice that we have a 1 in the denominator of our second fraction so we want to find a fraction that is equivalent to 70/5 that has a 1 in the denominator.
If we divide the numerator and the denominator of 70/5 by 5, we get the equivalent fraction 14/1 or
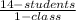 .
.
This means that the unit rate for 70 students in 5 classes is 14 students per class.
Unit rates can also be useful for solving the types of problems that I showed above.