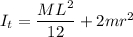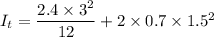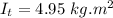Answer:
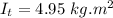
Step-by-step explanation:
Given that
L = 3 m
M = 2.4 kg
m=0.7 kg
r= L/2 = 1.5 m
The moment of inertia of rod about it center
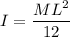
The moment of inertia of point mass about center of rod
I'= mr² + mr²
So total moment of inertia
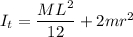
By putting the values