Question

A student claims that -4i is the only imaginary root of a quadratic polynomial equation that has real coefficients.

a. What is the student’s mistake? (2 points)
b. Write one possible polynomial that has the correct roots from part a in standard form. (3 points)

Answer 1

If a quadratic equation has an imaginary root -4i, then its conjugate i.e. 4i will be the other root of the equation.

`x^(2) + 16 = 0`

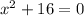
Explanation:

a. The only imaginary root of a quadratic equation is -4i, this is not possible.

Because, if a quadratic equation has an imaginary root -4i, then it's conjugate i.e. 4i will be the other root of the equation.

b. So, the two roots of a quadratic equation are imaginary and they are 4i and -4i.

Therefore, the equation will be

(x - 4i)(x + 4i) = 0

⇒
`x^(2) - (4i)^(2) = 0`

⇒
`x^(2) - (- 16) = 0`

⇒
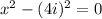
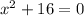`x^(2) + 16 = 0` (Answer)