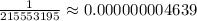Answer:
The required probability is
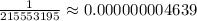
Explanation:
Consider the provided information.
If the eight numbers drawn match the numbers that a player had chosen, the player wins $1,000,000.
Determine the total number of ways 8 numbers can be drawn,
Since the order the numbers are drawn in does not matter the number of possible outcomes of the lottery drawing is :

Only one would match all 8 numbers on the player’s ticket,
Therefore, the probability of winning the grand prize is:
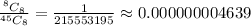
Hence, the required probability is