Question

A furniture manufacturer sells three types of products: chairs, tables, and beds. Chairs constitute 45% of the company's sales, tables constitute 35% of the sales, and beds constitute the rest. Of the company's chairs, 8% are defective and have to be returned to the shop for minor repairs, whereas the percentage of such defective items for tables and beds are 4% and 5% respectively. A quality control manager just inspected an item and the item was not defective. What is the probability that this item was a chair?

Answer 1

The probability that this non defective product is a chair is 44.04 %.

Explanation:

Given:

The probability of getting a product as chair is,
`P(A)=45\%=0.45`

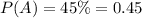
The probability of getting a product as table is,
`P(B)=35\%=0.35`

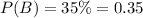
The probability of getting a product as bed is,
`P(C)=20\%=0.20`

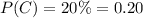
Now, let event D be having a defective product at random.

So, as per the question,

Probability of producing a defective product as chair is,
`P(D/A)=8\%=0.08`

Probability of producing a non defective product as chair is
`P(Not\ D/C)=100 - 8 = 92%=0.92`

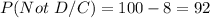
Probability of producing a defective product as table is,
`P(D/B)=4\%=0.04`

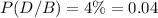
Probability of producing a defective product as bed is,
`P(D/C)=5\%=0.05`

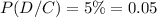
Now, probability of having a defective product when selected at random is given as:

`P(D)=P(A)\cdot P(D/A)+P(B)\cdot P(D/B)+P(C)\cdot P(D/C)\\P(D)=(0.45* 0.08)+(0.35* 0.04)+(0.20* 0.05)\\ P(D)=0.036+0.014+0.01\\P(D)=0.06`

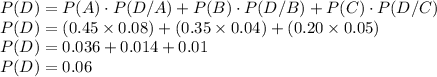
Now, probability of selecting a non defective product is = 1 - 0.06 = 0.94

Now, probability of selecting a product to be chair given that it is non defective is given using Bayes' Theorem and is given as:

`P(A/Not\ D)=(P(A)\cdot P(Not\ D/A))/(P(Not\ D))\\P(A/Not\ D)=(0.45* 0.92)/(0.94)=(0.414)/(0.94)=0.4404`

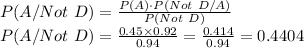
Therefore, the probability that this non defective product is a chair is 44.04 %