Question

The cell potential of a redox reaction occurring in an electrochemical cell under any set of temperature and concentration conditions can be determined from the standard cell potential of the cell using the Nernst equation E = E° − RT nF ln Q where E is the cell potential of the cell, E° is the standard cell potential of the cell, R is the gas constant, T is the temperature in kelvin, n is the moles of electrons transferred in the reaction, and Q is the reaction quotient. Use this relationship to answer the problem below. For the following oxidation-reduction reaction Ni2+(aq) + Zn(s) → Ni(s) + Zn2+(aq) the standard cell potential is 0.51 V. What is the actual cell potential of the cell if the temperature is 316 K, the initial Ni2+ concentration is 0.00104 M, and the initial Zn2+ concentration is 0.0141 M? (Note that the reaction involves the transfer of 2 moles of electrons, and the reaction quotient is 13.6.)

Answer 1

Answer : The actual cell potential of the cell is 0.47 V

Step-by-step explanation:

Reaction quotient (Q) : It is defined as the measurement of the relative amounts of products and reactants present during a reaction at a particular time.

The given redox reaction is :

`Ni^(2+)(aq)+Zn(s)\rightarrow Ni(s)+Zn^(2+)(aq)`

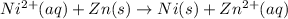
The balanced two-half reactions will be,

Oxidation half reaction :
`Zn\rightarrow Zn^(2+)+2e^-`

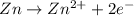
Reduction half reaction :
`Ni^(2+)+2e^-\rightarrow Ni`

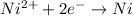
The expression for reaction quotient will be :

`Q=([Zn^(2+)])/([Ni^(2+)])`

In this expression, only gaseous or aqueous states are includes and pure liquid or solid states are omitted.

Now put all the given values in this expression, we get

`Q=((0.0141))/((0.00104))=13.6`

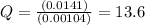
The value of the reaction quotient, Q, for the cell is, 13.6

Now we have to calculate the actual cell potential of the cell.

Using Nernst equation :

`E_(cell)=E^o_(cell)-(RT)/(nF)\ln Q`

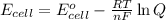
where,

F = Faraday constant = 96500 C

R = gas constant = 8.314 J/mol.K

T = room temperature = 316 K

n = number of electrons in oxidation-reduction reaction = 2 mole

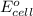`E^o_(cell)` = standard electrode potential of the cell = 0.51 V

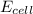`E_(cell)` = actual cell potential of the cell = ?

Q = reaction quotient = 13.6

Now put all the given values in the above equation, we get:

`E_(cell)=0.51-((8.314)* (316))/(2* 96500)\ln (13.6)`

`E_(cell)=0.47V`

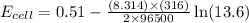
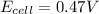
Therefore, the actual cell potential of the cell is 0.47 V