Question

Based on a random sample of 30 U.S. workers, a researcher found that the average (X¯) number of vacation days a U.S. worker takes per year is 16. The sample standard deviation (s) is 12 days. The goal is to construct a 99% confidence interval for the average (μ) number of vacation days taken by U.S. workers per year. Assume that the random variable, number vacation days taken by U.S. workers (denoted by X), is normally distributed.

The standard error (SE) of X¯ is

(A) 2.19
(B) 0.53
(C) 0.4
(D) 2.92

Answer 1

Answer: (A) 2.19

Explanation:

As per given , we have

Sample size : n= 30

Average number of vacation days a U.S. worker takes per year :
`\overline{x}=16`

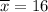
Sample standard deviation : s= 12

Significance level :
`\alpha= 1-0.99=0.01`

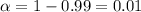
Degree of freedom : df= 29 (n-1)

The standard error(SE) of sample mean
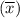`(\overline{x})` is given by :-

`SE=(s)/(√(n))\\\\=(12)/(√(30))=2.19089023002\approx2.19`

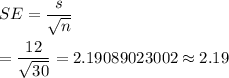
Hence, the standard error(SE) of sample mean
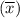`(\overline{x})` is 2.19.