Answer:
The area of the square when x = -2 and y = 2 is 256 sq. units.
Explanation:
The side of the square =
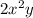
Now, AREA OF THE SQUARE = SIDE x SIDE
⇒ Area of the square is:
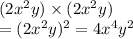
So, the area of the square is

Now, to find the area when x = -2 and y = 2
So,
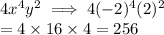
⇒The area of the square when x = -2 and y = 2 is 256 sq. units.