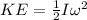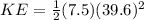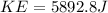Answer:
Part a)
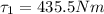
Part b)
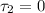
Part c)
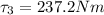
Part d)
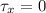
Part e)
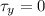
Part f)
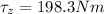
Part g)

Part h)
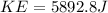
Step-by-step explanation:
Part a)
Torque due to F1 force is given as
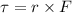
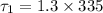
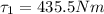
Part b)
Torque due to F2 force is given as
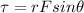
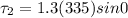
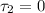
Part c)
Torque due to F3 force is given as
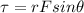
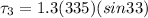
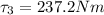
Part d)
Net torque along x direction is given as
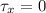
Part e)
Net torque along y direction is given as
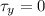
Part f)
Net torque along x direction is given as
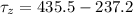
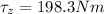
Part g)
angular acceleration is given as
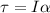
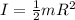
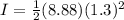
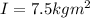
now we have


Part h)
angular speed of the disc after 1.5 s
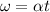
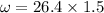
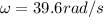
now rotational kinetic energy is given as