Answer:
The value of SecФ is
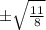 .
.
Explanation:
Given as for trigonometric function :
tan²Ф =
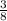
Or, tanФ =
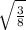
∵ tanФ =

So,
 =
=
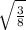
So, Hypotenuse² = perpendicular² + base²
or, Hypotenuse² = (
 )² + (
)² + (
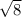 )²
)²
Or, Hypotenuse² = 3 + 8 = 11
Or, Hypotenuse = (
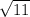 )
)
Now SecФ =
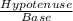
or, SecФ =
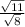 =
=
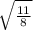
Second Method
Sec²Ф - tan²Ф = 1
Or, Sec²Ф = 1 + tan²Ф
or, Sec²Ф = 1 +
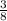
Or, Sec²Ф =

Or, SecФ =
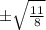
Hence The value of SecФ is
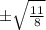 . Answer
. Answer